Diego R. Maltrana
Dr. Physics PUC.
There are texts in which theoretical analysis is done on colors, textures, and brush strokes to unveil what the artist intents to show through her work. They shed light on what is, though present, not evident to everyone. This article will try to do the exact opposite; pointing out precisely to what is obvious to the spectator but actually is not to be found.
Paraphrasing Huidobro: “The exhibition is a game of illusions, and not what you want to believe…”
In physics there are many instances where the attention is on seemingly trivial situations to begin with, and only by starting from there, can one unravel the problem and reach unexpected conclusions. In this text I will talk about a series of evident arguments to see where they take us.
The show is a sequence of 8 paintings, from the same place, evolving. The paintings are fragments of a sweetwater river, a place of thick vegetation, where by seeing a few branches one can deduce the existence of a forest.
In this river something has perturbed the water. This object could not have been too big or too different from a sphere. It could not have been, for example, a branch because the water shows concentric circles opening. This pattern similar to the one produced by a drop in a pool, defers enough from the splash of an extended object to be distinguished as such.
The painting sequence captures different stages of this movement. The waves spread and increase in radios until they fade out. In this case there is a double movement or dilution because as the waves start to gradually disappear, so is the color. Patricia Claro accentuates the feeling of change, making a subtle but undeniable reference to Heraclitus; despite the images being from the same place, the river is not the same.
In each of these paintings therefore, there are images of water moving. This phenomenon is enhanced by presenting it as a sequence. However, I believe this elaborate fiction to be product of our unconsciousness. What follows is the attempt to prove this belief.
The first evidence of the deception comes from the belief that these are images of water. However water is a transparent colorless substance and these properties cannot be depicted in a pictorial setup.
An image is a composition of light, and the light is captured by our senses as colors or white light (the sum of all colors). If light is the only thing that can be represented, we will try to understand what it is and what it means for something to be transparent and colorless. We will also try to find out how the images of something possessing both properties could be recreated.
When we talk about rays of light, we talk about objects that “travel” through space with a certain velocity. The use of the word “travel” implies that these objects come from a source, are produced at a point, and travel to reach another point where they eventually generate an image. Therefore the image is found at the end of the route.
An object is referred to as transparent if light can pass through it. Since the paintings don’t correspond to the image of the riverbed, we know that the light doesn’t come from the bottom and therefore has not passed through water. It is not the transparency of water which allows us to identify water in the paintings.
Practically no object in the nature emits light. Sun is the main source of light on earth.
The objects can be seen because when the white light from the sun collides with them, they absorb part of the wavelengths (part of the color spectrum) and emit the rest.
In a sense leaves of a tree are all colors but green. They absorb the rest of the colors except the one we see.
These kind of interactions between the light and objects is not true in the case of water because it doesn’t absorb part of light’s wavelengths so that the rest would bounce back (that’s why its colorless). When the light reaches the type of water represented in the sample, part of it penetrates and part of it gets reflected without a color being absorbed in particular.
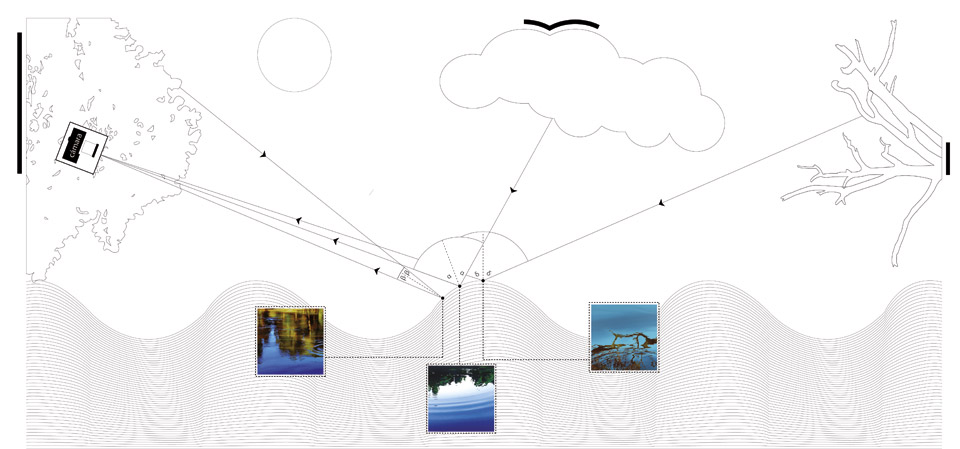
What allows us to “see” the water in these paintings should be associated with one of these two processes: reflection and refraction. Both correspond to a change in the direction of the propagation of bright light when it passes from a medium to another or when it meets the mentioned intersection. What makes it possible to create “paintings of water” in this case is only the mirror like characteristics of water and not both explained processes.
When an image is formed, that is to say when the rays of light cross each other or converge to a point on a screen (or on retina), there is no way to know if the rays were deflected from their original source. Light travels in a straight line so our brain assumes that it comes from objects separated from our eyes in a straight path. In other words there is no way to know if the image was reflected from a mirror or reaching our eyes directly from the object unless we see the edge of the mirror or have other additional information.
In the case of Claro’s paintings, water acts as a “particularly” deformed mirror. If the water was absolutely still when the photo was taken, it would have been impossible to decide whether it is the natural environment or its reflection. The only way to distinguish them would be to have the edges of the river or another identifiable element out of reflection in the photo.
But the type of water Claro paints is never still and this is significant in two ways: on the one hand, it allows us to “see” water we couldn’t otherwise see. On the other hand it tricks us into believing it has movement.
The fact that we see water and movement in the pictorial sequence, in my opinion, is a product of our brain. It is an elaborate delusion that requires our trained eyes as the spectators of the work.
We are able to see water because we have the experience of the deformation it can cause in the reflected images. These “particular deformations” have to propagate since they are deformations by a non-rigid surface with forces fighting to enter the equilibrium (liquid’s surface tension). In liquids, deformations don’t generate just any movement, but a very particular one. They “spread” in the medium creating waves mainly due to surface tension.
The physics of wave patterns at the surface of water is very complex and requires extensive mathematical explanation. Richard Feynman who received the Nobel prize (1965) for the development of quantum electrodynamics, and one of the greatest physicists of the last century would talk about how paradoxical it was for him to take water waves as an example to explain waves in general. He considered it to be a notorious problem that is more complex than other wave phenomenons.
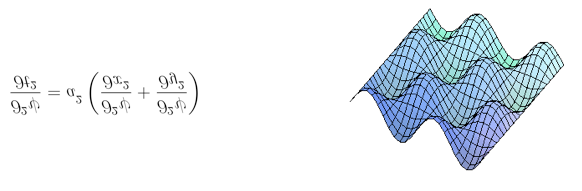
Despite the difficulties, it is enough to say that the deformations in water could be described by what is know in mathematics as the “wave function”. The equation is as follows.
Where ψ is a function of ‘x’, ‘y’ coordinates and of time ’t’, and ‘a’ is the velocity of wave propagation. Once function ψ is evaluated at a given position (x’,y’) and time (t’), I can obtain the number associated with the height (the z axis). With that, it is possible to determine the shape of the mantle at every point.
This is a second-order differential equation which means one must make use of the changes in the function (more precisely a change of the changes or their second derivatives).
What this differential equation tells us is that height variations with respect to time (left part of the equation) equals changes in the height with respect to spatial changes, to move in one direction or another (right side of the equation).
In other words the movement of a wave is proportional to its deformation. If there is deformation of the surface or different heights for different ‘x’ and ‘y’, then there will be movement or different values for its temporary exchange rate.
When we identify something as being deformed like the surface of water, our brain immediately recognizes movement on that surface. The waves always have to move according to our brain as they do in the equation.
In some of Claro’s paintings these waves appear as simple dark stripes followed by light ones with some in the shape of flattened ellipse. If you pay close attention there is not much more than stripes of contrasting color. Sometimes they are not even explicit ellipses, though our brain reconstructs them as movement of water.
Therefore it is only the mirror capacity of water that allows us to recognize it in the paintings. Clear zones are related to the reflection of the environment’s light portion. Dark stripes and stains in the water correspond to the reflection of the image in the other zones, such as part of the woods or a branch.
Where ψ is a function of ‘x’, ‘y’ coordinates and of time ’t’, and ‘a’ is the velocity of wave propagation. Once function ψ is evaluated at a given position (x’,y’) and time (t’), I can obtain the number associated with the height (the z axis). With that, it is possible to determine the shape of the mantle at every point.
This is a second-order differential equation which means one must make use of the changes in the function (more precisely a change of the changes or their second derivatives).
What this differential equation tells us is that height variations with respect to time (left part of the equation) equals changes in the height with respect to spatial changes, to move in one direction or another (right side of the equation).
In other words the movement of a wave is proportional to its deformation. If there is deformation of the surface or different heights for different ‘x’ and ‘y’, then there will be movement or different values for its temporary exchange rate.
When we identify something as being deformed like the surface of water, our brain immediately recognizes movement on that surface. The waves always have to move according to our brain as they do in the equation.
In some of Claro’s paintings these waves appear as simple dark stripes followed by light ones with some in the shape of flattened ellipse. If you pay close attention there is not much more than stripes of contrasting color. Sometimes they are not even explicit ellipses, though our brain reconstructs them as movement of water.
Therefore it is only the mirror capacity of water that allows us to recognize it in the paintings. Clear zones are related to the reflection of the environment’s light portion. Dark stripes and stains in the water correspond to the reflection of the image in the other zones, such as part of the woods or a branch.

In order for the rays of light from different zones of the environment to converge to a single point (our retina), the perpendicular angle of the reflected light to the surface, we call that normal, must change. This gives evidence to deformation. Our brain immediately associates this deformation with movement.
If the surface which reflects the image is deformed, it will generate discontinuity in the original image. We are used to seeing a piece of the sky standing in the reflection of a tree, or to see its image in pieces when we look at its reflection in clear water of a river or a lake. Without having this experience it would probably be impossible to see the presence of water in Claro’s work.
Water and movement arise from a fragmented familiar image. The paintings of Patricia Claro present an abstraction of this fragmentation. By creating depth and using masks, she makes up an image which generates sensations about things that in my opinion are not possible to be painted.